Data-integrated Simulation Science often requires the fit of model outputs to experimental data. This can be achieved by properly choosing free model parameters and in the best case, this parameter estimation even enables scientific reasoning. The most fundamental way to solve this parameter estimation task is by first defining an error function between simulation output and experimental data, and second, minimizing said error. The resulting parameter point
estimate, while being a good first guess, is still lacking some desirable properties. For example, it does not indicate whether the found result is the only good one or how sensitive it is with respect to measurement noise. In addition, the
definition of meaningful error functions is a challenging modeling task by itself. Probabilistic inference methods like Bayesian parameter inference circumvent some of the issues mentioned above by returning a probability distribution over all parameters that inherently indicates ambiguities and quantifies uncertainties. However, it still relies on a suitable likelihood function or distribution distance measure in the likelihood-free case.
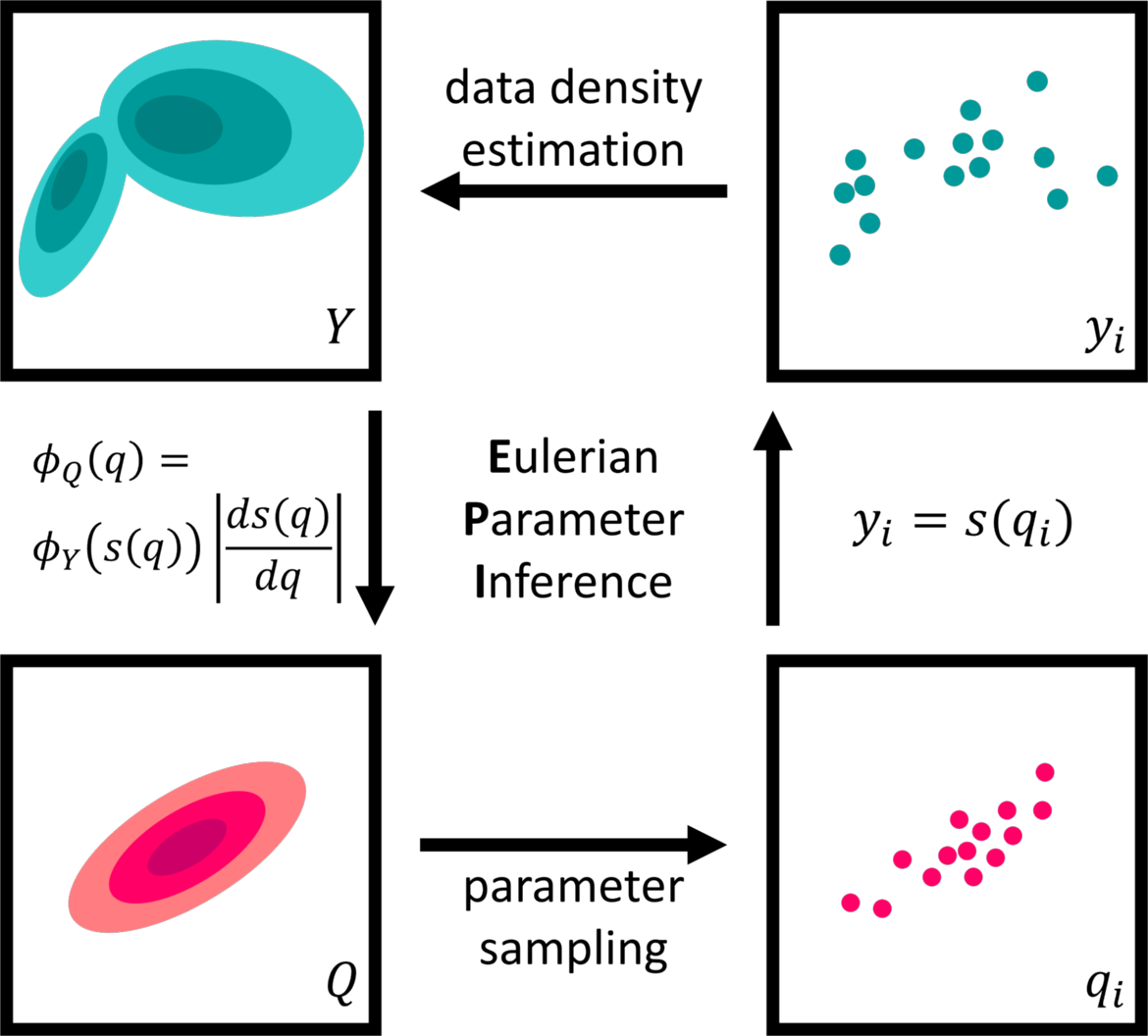
With Eulerian Parameter Inference (EPI), we presented an intuitive, mathematically well-founded parameter estimation method that returns a parameter distribution that is in accordance with experimental data for a given, deterministic simulation model. It does not require the definition of any kind of error, likelihood, or distance function and only used evaluations of the model and its derivative during the parameter estimation task. At its core, EPI interprets the measurement data {yi}i=1...n as a sample of an underlying data random variable Y. Using the deterministic simulation model s, the data density ϕY is transformed to become a parameter density ϕQ. Each pointwise evaluation of the parameter density only requires the result of one simulation and simulation derivative. The figure below visualizes EPI concisely.
We already presented the successful implementation of EPI for several academic examples. Now, our ambitious goal is to generalize EPI towards being a black-box method for general modeling applications. However, there are still challenges to tackle on this way. Specifically, we are currently investigating different kinds of heterogeneous data and how EPI can be used to optimally extract included information. Furthermore, modern sampling techniques are
employed to use as few simulation evaluations as possible during the inference task in order to be computationally efficient. A third interesting area is the generalization of EPI towards non-deterministic simulation models.
EPI on GitHub
Clone and contribute to our GitHub Project!
EPI Tutorial
Our Tutorial: the fastest way to try EPI yourself!

Vincent Wagner
M.Sc.Research Assistant